ホイールのスポーク長・左右テンション比の計算方法

左右非対称のリアホイールの算出方法が分かれば、左右対称のフロントについても計算が可能です。

ホイールの幾何学的図面

ホイール側面から見たときの考察

横から見たスポークの長さLは、ERDやPCDを使うと以下の図で示すことができます。

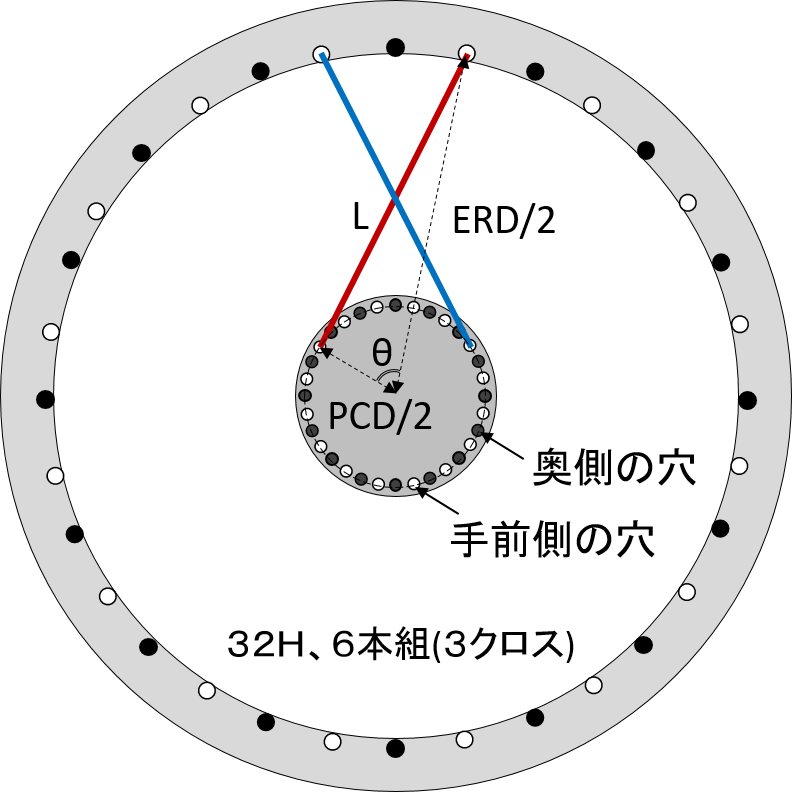
スポークを垂直に見たときの考察

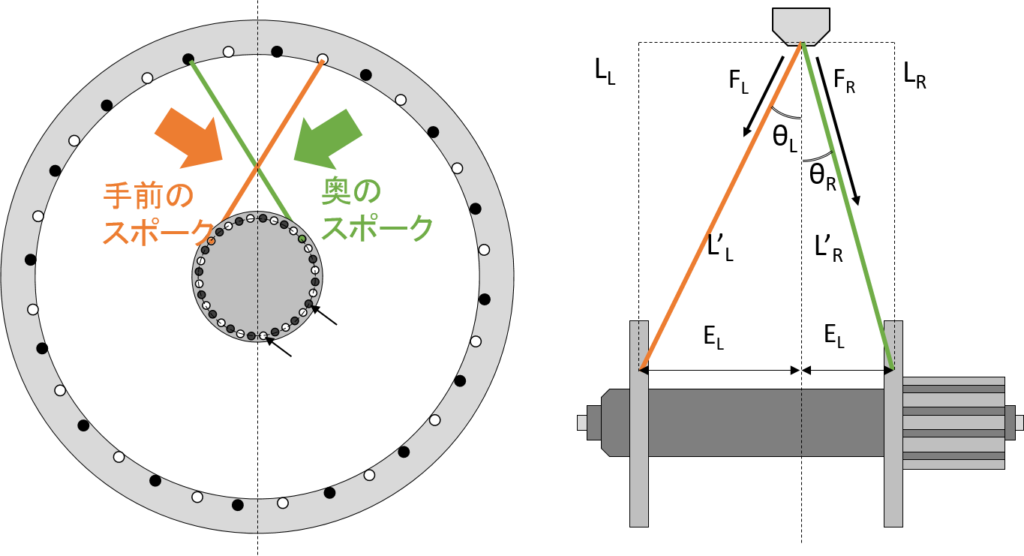
それぞれを矢印の方からみて合成すると、右図のようになります。手前のスポークと奥のスポークは同じ本数あり、一本あたりのFLとFRの左右方向の分力は釣り合っています。

スポーク長

横から見たときのθは穴数(N)とクロス数(C)を用いて次式で表せます。

Lについては数学的な知識（余弦定理）を使って次式で表せます。

この値の平方根を取ればLの長さがわかります。

補正したフランジセンター間距離Eの長さが分かっているので、スポーク長L’を求めましょう。

これが幾何学的な長さです。実際に使用するスポーク長L”は、スポークテンションによる伸びを考慮する必要があります。

伸びδ[mm]は

Nはスポークテンション、DT swissチャンピオン2mmとの重量比をwとすれば、

と表すことができます。wは以下の値を使ってください。

• DT swiss チャンピオン2mm → 1
• DT swiss コンペティション → 0.86

伸びδ[mm]は700Cなら0.2~0.9mm程度になります。したがって、実際に使用するスポーク長L”は次式で算出することができます。

ブレース角

正面から見たときのスポークの角度（ブレース角）θも求めることができます。

スポークテンションの左右比

FLとFRの左右方向の分力は釣り合っているので、

ここで以下の関係がある。

したがって、

つまり、

ER/ELを大きくする → オフセットリムを利用する

1. ERはどれも大差ない
2. ELを小さくすると横剛性が落ちる

ほとんどの完組みホイールにおいて、左の横剛性確保のために、左右のスポークテンションのバランスが悪くなろうとも、左フランジ幅は狭く設計されていません。つまり、方法１や方法２は採用せず、「ひどいオチョコ」のままで なんとか左右のテンションバランスを均等に近づける工夫をとっています。

唯一の解決策はオフセットリム（アシンメトリックリム）を利用することです。入手用意なオフセットリムでオススメなのは以下の通りです。

• KINLIN　XR-22T クリンチャー (445g)
• RR411 Asymmetric チューブレスレディ (435g)
•  

LR’/LL’を小さくする＝実用的である

• LRを小さくするために２クロスにする
• LLを大きくするために３・４クロスにする
• ハイローフランジハブうを使用する

ハイローフランジハブは、右側のフランジを左側のフランジよりも大きくした後輪ハブです。カセットスプロケットの存在によって小さくなる右スポークのプレース角を大きくして、車輪の横強度を大きくする意図がある。 左右のスポークの張力差は少なくなる。

引張応力比

スポークの平均断面積は重量比に比例します。

つまり応力比σL/σRは

σL/σR=(FL/FR)/(wL/wR)

材料力学的に議論してみましょう。

実売ホイールのスポークテンションの左右比（計算中）

では実際に販売されているものたちのスポークテンションの左右比FL/FRの値がどんなものかを計算的に算出していきましょう。